Roots of Non-Linear Equation

Any equation whose slope is not constant for all possible input values is called a non-linear equation. In other words, any equation that doesn't represent a line, a plane or a hyperplane is a non-linear equation. This includes a wide variety of equations with different characteristics.

The root of a non-linear equation is the point where the equation evaluates to zero. For explicit equations such as $y=f(x)$, we find the root by equating $f(x)=0$. Similarly, for implicit equations such as $f(x,y)=0$, we find the root by equating $f(x,y)=0$.

A non-linear equation may or may not have a root. Some non-linear equations have more than one root while some have infinitely many roots.

Examples of Non-Linear Equation

The equation $y=\sin x$ has an infinite number of roots when y=0

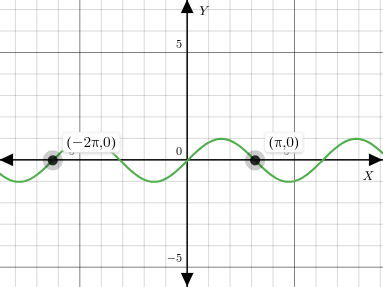
Plot of y=sin(x).

A circle has a finite number of roots for both $y=0$ and $x=0$ but doesn't pass the vertical line test.

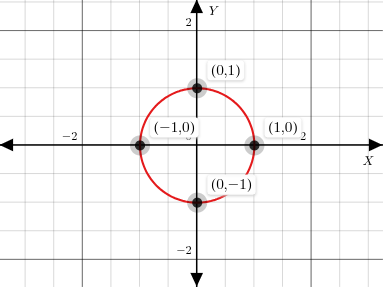
Plot of $x^2+y^2=1$ (Circle).

A parabola has a finite number of roots and does pass the vertical line test. In general explicit equations pass the vertical line test.

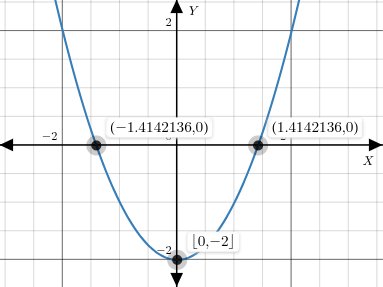
Plot of $y=x^2-2$ (Parabola).

Root Finding Algorithms

There are many root-finding algorithms for non-linear equations. All of these methods are iterative and require one or more initial guesses. Some methods can find roots of explicit equations while some can find roots of both explicit and implicit equations.

Some of the most popular methods of finding roots are:

1. Bisection Method
2. Secant Method
3. Newton-Raphson Method
4. Fixed Point Iteration Method
5. Point Algorithm (For both implicit and explicit)

We will go into the details of all of these methods in the coming articles.