Newton-Raphson Method

The Newton-Raphson is one of the fastest methods of finding roots of equations. This method was independently developed by both Sir. Issac Newton and Joseph Raphson.

This method requires only one initial guess and thus belongs to the open bracket category. The initial guess needs to be near the solution otherwise the method may not converge.

This method requires the analytical derivative of the function. We can also approximate the derivative of the function with numerical calculation but the results will be inferior.

We can better understand the Newton-Raphson method visually with the following diagram:

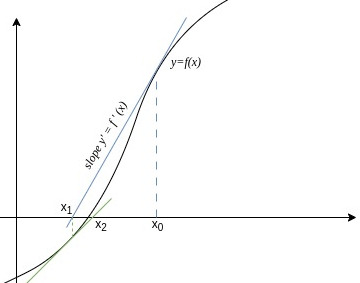
Given an initial guess, $x_0$ that is fairly near to the solution, we approximate the solution as the intersection between the tangent at $x_0$ and the x-axis. This point of intersection will be:

$$x_1 = x_0 - \frac{f(x_0)}{f'(x_0)}$$

We then take $x_1$ as the initial guess and repeat the operation until the error is less than the threshold value.

Algorithm

1. Start
2. Read $x_0$ and error threshold $e$
3. Declare variable $x$
4. Calculate $x=x_0-f(x_0)/f'(x_0)$
5. If $|x-x_0|> e$ then assign $x_0=x$ and goto 4.
6. Print the solution $x$.
7. Stop

Programs

C

/*
* Newton-Raphson Method in C
*/

#define MAX_ITER 100
#define DEL 1e-8
#include<stdio.h>
#include<math.h>

double f(double x){
  return x*x+x-2;
}

double f_prime(double x){
  return 2*x+1;
}


// Numerical derivative
// Useful when it is difficult to obtain analytical derivative
double f_prime_num(double x){
  return (f(x+DEL)-f(x))/DEL;
}

int main(){
  double x, x0, threshold;
  int iter = 0;
  printf("-----------Newton-Raphson Method-----------\n");
  printf("Enter the initial guess x0: ");
  scanf("%lf", &x0);

  printf("Enter the error threshold: ");
  scanf("%lf", &threshold);

  printf("%10s %10s %10s\n", "N", "xn", "xn+1");
  while(iter < MAX_ITER)
  {

    x = x0 - f(x0)/f_prime(x0);
    iter++;
    printf("%10d %10.5lf %10.5lf\n", iter, x0, x);
    if(fabs(x-x0)<threshold){
      printf("\nHence the solution is: %10.5lf\n", x);
      return 0;
    }
    x0=x;
  }

  printf("Max iterations reached\n");
  return -1;
}

Python

## Newton-Raphson Method in C

MAX_ITER = 100


def f(x):
    return x*x+x-2


def f_prime(x):
    return 2*x+1


def nr(x0, threshold):
    iter = 0
    print("%10s %10s %10s" % ("N", "xn", "xn+1"))
    while iter < MAX_ITER:
        x = x0 - f(x0)/f_prime(x0)
        iter += 1
        print("%10d %10.5lf %10.5lf" % (iter, x0, x))

        if abs(x-x0) < threshold:
            print("\nHence the solution is %10.5f" % x)
            return

        x0 = x

    raise "Max iterations reached"


print("-----------Newton-Raphson Method-----------")
x0 = float(input("Enter the initial guess x0: "))
threshold = float(input("Enter the error threshold: "))
nr(x0, threshold)

Matlab

%% Newton-Raphson method in Matlab/Octave

MAX_ITER = 100;

f = @(x) x*x+x-2;
f_prime = @(x) 2*x+1;

printf('-----------Newton-Raphson Method-----------\n');

printf('Enter the initial guess x0: ');
x0 = scanf('%f', 'C');

printf('Enter the error threshold: ');
threshold = scanf('%f', 'C');

printf('%10s %10s %10s\n', 'N', 'xn', 'xn+1');
iter = 0;
while(iter < MAX_ITER)
  x = x0 - f(x0)/f_prime(x0);
  iter++;
  printf('%10d %10.5f %10.5f\n', iter, x0, x);

  if(abs(x-x0)<threshold)
    printf('\nHence the solution is: %10.5f\n', x);
    break;
  endif
  
  x0=x;
end

if(iter>=MAX_ITER)
  error('Max iterations reached\n');
end

Output

-----------Newton-Raphson Method-----------
Enter the initial guess x0: 0
Enter the error threshold: 0.001
         N         xn       xn+1
         1    0.00000    2.00000
         2    2.00000    1.20000
         3    1.20000    1.01176
         4    1.01176    1.00005
         5    1.00005    1.00000

Hence the solution is:    1.00000

Convergence

The Newton-Raphson method is not guaranteed to converge. When the root is far away from the initial guess, this method may drift away and converge to another root. If there is a minima or a maxima at the solution then this method will oscillate about the solution and never converge. Due to the less stability, this method is used only after an approximate solution is found using other methods.

The rate of convergence of this method is variable and the order of convergence is 2. The successive error can be obtained as:

$$e_{n+1} = c_n \cdot e_n^2$$

Where $c_n$ is different for each iteration and depends upon the curvature and slope of the function. Due to the quadratic order of convergence, this method converges very fast especially when near to the solution.

Advantages

1. The Netwon-Raphson method is one of the fastest methods because of its quadratic order of convergence.
2. Simpler to implement if the derivative is already known.
3. Requires only one initial guess

Disadvantages

1. Requires derivative of the function. In some cases, the analytical derivative may have long expression resulting in a large number of calculations.
2. The convergence is unstable and may drift if the initial guess is not near the solution.
3. If there is an extrema at the solution then there will be an infinite oscillation.
4. Repeated values of $x_n$ will cause infinite oscillation. The value of $x_n$ repeats when two tangents intersect at the same point in the x-axis.
5. If the first derivative $f'(x)$ is close to zero then this method will not converge.