Fixed Point Iteration Method

In the fixed point iteration method, we are given with function $y=f(x)$. We reorganize this function into the form:

$$x=\phi(x)$$

The function $\phi(x)$ is called a fixed point iteration function.

After obtaining the function $\phi(x)$, we have to find a numerical value of $x$ such that $x=\phi(x)$. For that, we start with a guess $x_0$. Then we iteratively find the next approximation with:

$$x_{n+1} = \phi(x_n)$$

This is equivalent to applying the function over and over again to the initial guess like $\phi(\phi(\phi(x_0)))$. We can understand why this works with the following diagram:

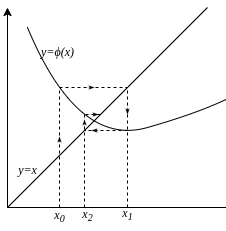
Fixed point iteration visualization

In the above diagram, the vertical projection into $y=\phi(x)$ is equivalent to calculating $\phi(x_n)$ and the horizontal projection into the line $y=x$ turns the output of $\phi(x_n)$ to be the next input producing $\phi(x_{n+1})$.

The fixed point iteration method is one of the oldest and most widely used methods. Babylonians used this method to find the square root of a number.

Given, the function $y=x^2-N$, finding the square root of $N$ is equivalent to solving $x^2-N=0$. Now let's write this equation in the form $x=\phi(x)$ as:

$$x^2-N=0$$ $$\text{or, } x = \frac{N}{x}$$ $$\text{or, } x + x = \frac{N}{x} + x$$ $$\therefore x=\frac{1}{2}\left( \frac{N}{x} + x \right)$$

Now we can find the square root of $N=2$ starting from $x_0=1$ as follows:

$$x_1 = \frac{1}{2}\left( \frac{2}{1} + 1 \right) = 1.5$$ $$x_2 = \frac{1}{2}\left( \frac{2}{1.5} + 1.5 \right) = 1.4167$$ $$x_3 = \frac{1}{2}\left( \frac{2}{1.4167} + 1.4167 \right) = 1.4142$$

Algorithm

1. Start
2. Read values for initial guess $x_0$ and error threshold $e$
3. Calculate $x_1=\phi(x_0)$
4. If $|x_1-x_0|>e$ assign $x_0=x_1$ and go to 3.
5. Print solution $x_1$
6. Stop

Programs

C

/*
* Fixed point iteration method in C
*/
#include<stdio.h>
#include<math.h>
#define MAX_ITER 100

double phi(double x){
  return 0.5 * (2/x + x);
}

int main(){
  double x0, x1, threshold;
  int iter = 0;
  printf("-------------Fixed Point Iteration-------------\n");
  
  printf("Enter x0: ");
  scanf("%lf", &x0);

  printf("Enter error threshold: ");
  scanf("%lf", &threshold);

  printf("%5s %10s %10s\n", "N", "xn", "xn+1");
  while(iter<MAX_ITER){
    x1 = phi(x0);
    iter++;

    printf("%5d %10.5lf %10.5lf\n", iter, x0, x1);
    if(fabs(x1-x0)<threshold){
      printf("\nHence the solution is: %10.5lf\n", x1);
      return 0;
    }else{
      x0 = x1;
    }
  }

  printf("Max iterations reached\n");
  return -1;
}

Python

#
# Fixed point iteration method in Python
#

MAX_ITER = 100


def phi(x):
    return 0.5 * (2/x + x)


def fixed_point(x0, threshold):
    print("%5s %10s %10s" % ("N", "xn", "xn+1"))
    iter = 0
    while iter < MAX_ITER:
        x1 = phi(x0)
        iter += 1

        print("%5d %10.5lf %10.5lf" % (iter, x0, x1))
        if abs(x1-x0) < threshold:
            print("\nHence the solution is: %10.5lf" % x1)
            return
        else:
            x0 = x1

    raise "Max iterations reached"


print("-------------Fixed Point Iteration-------------")
x0 = float(input("Enter x0: "))
threshold = float(input("Enter error threshold: "))
fixed_point(x0, threshold)

Matlab

%% Fixed point iteration method in Matlab/Octave

MAX_ITER = 100;
printf('-------------Fixed Point Iteration-------------\n');

phi = @(x) 0.5 * (2/x + x);

printf('Enter x0: ');
x0 = scanf('%f', 'C');

printf('Enter error threshold: ');
threshold = scanf('%lf', 'C');

printf('%5s %10s %10s\n', 'N', 'xn', 'xn+1');
iter = 0;
while(iter<MAX_ITER)
  x1 = phi(x0);
  iter++;
  printf('%5d %10.5f %10.5f\n', iter, x0, x1);
  if(abs(x1-x0)<threshold)
    printf('\nHence the solution is: %10.5f\n', x1);
    break;
  else
    x0 = x1;
  end
end

if iter >= MAX_ITER
  error('Max iterations reached');
end

Output

-------------Fixed Point Iteration-------------
Enter x0: 1
Enter error threshold: 0.0001
    N         xn       xn+1
    1    1.00000    1.50000
    2    1.50000    1.41667
    3    1.41667    1.41422
    4    1.41422    1.41421

Hence the solution is:    1.41421

Convergence

The fixed point iteration method has a variable convergence rate and a linear order of convergence.

Advantages

1. Requires only one initial guess
2. Can be implemented easily in programs
3. Suitable for manual calculation

Disadvantage

1. Slower convergence.
2. Finding $\phi(x)$ can be challenging for complicated equations.