Bisection Method

In the bisection method, we start with an interval containing a solution. Then we divide the interval into two halves. Among these halves, one will contain the solution while the other will not contain the solution. We then choose the interval containing the solution and repeat dividing until the interval becomes small enough i.e. the distance between the two points is less than a threshold.

The bisection method fails to find the solution when the initial interval doesn't bracket any solution. This method belongs to the bracketing category as it requires the solution to be enclosed inside the interval.

It is used to find the roots of an explicit equation in one variable i.e. the equations of the form $y=f(x)$.

Concept of Bracketing

If $f(x)$ is continuous inside an interval $[a,b]$ and $f(a)\cdot f(b)< 0$ then there exists at least one root inside the interval $[a,b]$ where $f(x)=0$. The condition $f(a)\cdot f(b)< 0$ just tells us that the function has different signs at $x=a$ and $x=b$.

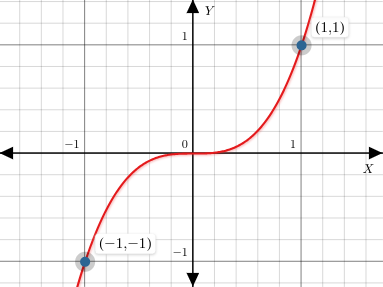
Plot of $y=x^3$

In the above plot, we can see that for left point $f(-1)=-1$ and for right point $f(1)=1$. The interval $[-1,1]$ does contain a solution at $x=0$. Intuitively, if a function changes its sign between two $x$ values and it is continuous then, the curve of the function must pass through the x-axis where its output will be zero i.e. $f(x)=0$.

But if the curve is not continuous despite satisfying $f(a)\cdot f(b)< 0$, then there may or may not be a solution inside the interval. For example:

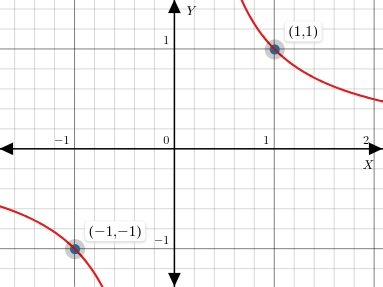
Plot of $y=1/x$

In the above plot, we can see that the function $f(x)=1/x$ is discontinuous at $x=0$ but it does satisfy $f(a)\cdot f(b)< 0$. If we operate the bisection method with $a=-1$ and $b=1$, the method will converge at $x=0$ but the condition $f(x)=0$ won't be satisfied as $f(0)=\infty$.

Algorithm

The algorithm for bisection method can be written as:

1. Start
2. Read $a$, $b$, $e$ (Error threshold) and $N$ (Maximum number of iterations).
3. Calculate $f_a=f(a)$ and $f_b=f(b)$
4. If $f_a\cdot f_b>0$, then $[a,b]$ doesn't bracket the solution, hence print the error and go to step 10.
5. Declare $x$ and $f_x$
6. Calculate $x=(a+b)/2$ and $f_x=f(x)$
7. If $f_a\cdot f_x< 0$ then assign $b\leftarrow x,f_b\leftarrow f_x$, else assign $a\leftarrow x,f_a\leftarrow f_x$.
8. If $|(a-b)/2| \ge e$ go to step 6.
9. Print solution $(a+b)/2$
10. Stop

How to change the interval?
When $f_x\cdot f_a< 0$, this means $[a, x]$ satisfies the bracketing criteria so we assign $b\leftarrow x$ and $f_b\leftarrow f_x$. Else $[x,b]$ satisfies the bracketing criteria so we assign $a\leftarrow x$ and $f_a\leftarrow f_x$.

Programs

C

/**
* Bisection method in C
*/
#include <stdio.h>
#include <math.h>
#define MAX_ITER 100

double f(double x)
{
  return x * x - 2;
}

int main()
{
  double a, b, threshold;
  double x, fx, fa, fb;
  int iter = 0;
  printf("---------Bisection Method---------\n");
  printf("Enter a: ");
  scanf("%lf", &a);
  printf("Enter b: ");
  scanf("%lf", &b);
  fb = f(b);
  fa = f(a);

  // Check whether the interval brackets a solution
  if (fa * fb >= 0)
  {
    printf("The given interval doesn't bracket a solution\n");
    return -1;
  }

  printf("Enter error threshold: ");
  scanf("%lf", &threshold);

  printf("\nSolution:\n");
  printf("%4s %10s %10s %10s %10s %10s %10s\n", "N", "a", "b", "f(a)", "f(b)", "x", "f(x)");

  // Perform bisection method
  while (fabs(a - b) / 2.0 > threshold && iter < MAX_ITER)
  {
    x = (a + b) / 2;
    fx = f(x);

    printf("%4d %10.5lf %10.5lf %10.5lf %10.5lf %10.5lf %10.5lf\n", iter + 1, a, b, fa, fb, x, fx);

    // Reassign the interval
    if (fa * fx < 0)
    {
      b = x;
      fb = fx;
    }
    else
    {
      a = x;
      fa = fx;
    }

    iter++;
  }

  printf("\nHence, the solution is: %10.5lf\n", (a + b) / 2.0);

  return 0;
}

Python

#
# Bisection method in Python
#

MAX_ITER = 100


def f(x):
    return x*x - 2


def bisection(a, b, threshold):
    fa = f(a)
    fb = f(b)

    # Check whether the interval brackets a solution
    if fa*fb >= 0:
        raise "The given interval doesn't bracket a solution"

    iter = 0
    print("\nSolution:")
    print("%4s %10s %10s %10s %10s %10s %10s" %
          ("N", "a", "b", "f(a)", "f(b)", "x", "f(x)"))
    while abs(a-b)/2 > threshold and iter < MAX_ITER:
        x = (a+b)/2
        fx = f(x)
        print("%4d %10.5f %10.5f %10.5f %10.5f %10.5f %10.5f" %
              (iter+1, a, b, fa, fb, x, fx))
        
        if fa * fx < 0:
            b, fb = x, fx
        else:
            a, fa = x, fx

        iter = iter + 1

    print("\nHence, the solution is: %10.5lf" % ((a+b)/2))


print("---------Bisection Method---------")
a = float(input("Enter a: "))
b = float(input("Enter b: "))
threshold = float(input("Enter error threshold: "))

bisection(a, b, threshold)

Matlab

%% Bisection Method in matlab/octave

MAX_ITER = 100;

% Declare the function
f = @(x) x*x-2;

printf('---------Bisection Method---------\n');

printf('Enter a: ');
a = scanf('%f', 'C');
printf('Enter b: ');
b = scanf('%f', 'C');

fa = f(a);
fb = f(b);

% Check whether the interval brackets a solution
if (fa * fb >= 0)
  error('The given interval doesn''t bracket a solution\n');
end

printf('Enter error threshold: ');
threshold = scanf('%f', 'C');


printf('\nSolution:\n');
printf('%4s %10s %10s %10s %10s %10s %10s\n', 'N', 'a', 'b', 'f(a)', 'f(b)', 'x', 'f(x)');

iter = 0;

% Perform bisection method
while (abs(a - b) / 2.0 > threshold && iter < MAX_ITER)
  x = (a + b) / 2;
  fx = f(x);
  printf('%4d %10.5f %10.5f %10.5f %10.5f %10.5f %10.5f\n', iter + 1, a, b, fa, fb, x, fx);
  
  % Reassign the interval
  if (fa * fx < 0)
    b = x;
    fb = fx;
  else
    a = x;
    fa = fx;
  endif

  iter++;
end

printf('\nHence, the solution is: %10.5f\n', (a + b) / 2.0);

Output

---------Bisection Method---------
Enter a: 1
Enter b: 2
Enter error threshold: 0.001

Solution:
   N          a          b       f(a)       f(b)          x       f(x)
   1    1.00000    2.00000   -1.00000    2.00000    1.50000    0.25000
   2    1.00000    1.50000   -1.00000    0.25000    1.25000   -0.43750
   3    1.25000    1.50000   -0.43750    0.25000    1.37500   -0.10938
   4    1.37500    1.50000   -0.10938    0.25000    1.43750    0.06641
   5    1.37500    1.43750   -0.10938    0.06641    1.40625   -0.02246
   6    1.40625    1.43750   -0.02246    0.06641    1.42188    0.02173
   7    1.40625    1.42188   -0.02246    0.02173    1.41406   -0.00043
   8    1.41406    1.42188   -0.00043    0.02173    1.41797    0.01064
   9    1.41406    1.41797   -0.00043    0.01064    1.41602    0.00510

Hence, the solution is:    1.41504

Convergence

In this method, the interval is divided by 2 in each step. This means the error decreases by a constant factor of $1/2$ after each step.

$$e_{n+1}=e_{n}/2$$

Since the factor $1/2$ is constant, we say that the convergence rate of the bisection method is constant. While the order of convergence is 1 or linear as $e_{n+1}$ is proportional to $e_n$ raised to the power 1.

Advantages

1. It is a stable method and doesn't drift away from the solution given the required initial conditions are met.
2. This method is guaranteed to converge and doesn't cause infinite loops.
3. It is easier to implement and understand.

Disadvantages

1. Slower convergence rate.
2. Requires initial interval to contain the solution.