Method of False Position

This method is an improvement over the bisection method. Like the bisection method, we start with an interval containing a solution. But instead of dividing the interval into two halves, we find the approximate solution by linear interpolation.

We call this method "false position method" because after each step an approximate(false) solution is calculated via linear interpolation. It is also called as Regula Falsi method. This method also requires the curve of function to be continuous inside the initial interval.

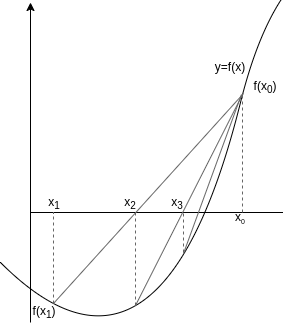
Method of False Position Graphical demonstration

Just like the bisection method, we start with two values $x_0$ and $x_1$ such that $f(x_0)\cdot f(x_1)< 0$. After this, we find the next solution as the intersection between the x-axis and the line joining $(x_0,f(x_0))$ and $(x_1,f(x_1))$ whose equation will be:

$$\begin{equation} y-f(x_0) = \frac{f(x_1)-f(x_0)}{x_1-x_0}(x-x_0) \end{equation}$$

Assigning $y=f(x)=0$ and simplifying above, we get:

$$\begin{equation} x = x_0-\frac{(x_1-x_0)f(x_0)}{f(x_1)-f(x_0)} \end{equation}$$

We will be using this formula of $x$ to find the next value of $x$. In the bisection method, we calculated new $x=(x_1+x_0)/2$ but in this method we calculate new $x$ with $eq^n(2)$.

Algorithm

The algorithm for bisection method can be written as:

1. Start
2. Read $x_0$, $x_1$, $e$ (Error threshold) and $N$ (Maximum number of iterations).
3. Calculate $f_{x_0}=f(x_0)$ and $f_{x_1}=f(x_1)$
4. If $f_{x_0}\cdot f_{x_1}>0$, then $[x_0,x_1]$ doesn't bracket the solution, hence print the error and go to step 11.
5. Declare $x$, $f_x$, $x_{prev}$ and $c=0$
6. Calculate $x=x_0-\frac{(x_1-x_0)f(x_0)}{f(x_1)-f(x_0)}$ and $f_x=f(x)$
7. If $f_{x_0}\cdot f_x< 0$ then assign $x_1\leftarrow x,f_{x_1}\leftarrow f_x$, else assign $x_0\leftarrow x,f_{x_0}\leftarrow f_x$.
8. If $c>0$ and $|x_{prev}-x|< e$ then goto step 9.
9. Assign $x_{prev}\leftarrow x$, $c\leftarrow c+1$ and goto step 6.
10. Print solution $x$.
11. Stop

Programs

C

/**
 * Method of False Position in C
 */
#include <stdio.h>
#include <math.h>
#define MAX_ITER 100

double f(double x)
{
  return x * x - 2;
}

int main()
{
  double x0, x1, threshold;
  double x, x_prev=NAN, fx, fx0, fx1;
  int iter = 0;
  printf("---------Method of False Position---------\n");
  printf("Enter x0: ");
  scanf("%lf", &x0);
  printf("Enter x1: ");
  scanf("%lf", &x1);
  fx1 = f(x1);
  fx0 = f(x0);

  // Check whether the interval brackets a solution
  if (fx0 * fx1 >= 0)
  {
    printf("The given interval doesn't bracket a solution\n");
    return -1;
  }

  printf("Enter error threshold: ");
  scanf("%lf", &threshold);


  printf("\nSolution:\n");
  printf("%4s %10s %10s %10s %10s %10s %10s\n", "N", "x0", "x1", "f(x0)", "f(x1)", "x", "f(x)");

  // Perform method of false position
  while (iter < MAX_ITER)
  {
    x = x0 - (x1 - x0) * fx0 / (fx1 - fx0);
    fx = f(x);

    printf("%4d %10.5lf %10.5lf %10.5lf %10.5lf %10.5lf %10.5lf\n", iter + 1, x0, x1, fx0, fx1, x, fx);

    // Reassign the interval
    if (fx0 * fx < 0)
    {
      x1 = x;
      fx1 = fx;
    }
    else
    {
      x0 = x;
      fx0 = fx;
    }

    if (iter > 0 && fabs(x_prev - x) < threshold)
    {
      // Check for the error after at least one iteration is done
      printf("\nHence, the solution is: %10.5lf\n", x);
      return 0;
    }

    iter++;
    x_prev = x;
  }

  printf("Max Iterations reached");
  return -1;
}

Python

#
# Method of False Position in Python
#

MAX_ITER = 100


def f(x):
    return x*x - 2


def false_position(x0, x1, threshold):
    x_prev = float('nan')
    fx0 = f(x0)
    fx1 = f(x1)

    # Check whether the interval brackets a solution
    if fx0*fx1 >= 0:
        raise "The given interval doesn't bracket a solution"

    iter = 0
    print("\nSolution:")
    print("%4s %10s %10s %10s %10s %10s %10s" %
          ("N", "x0", "x1", "f(x0)", "f(x1)", "x", "f(x)"))
    while iter < MAX_ITER:
        x = x0-(x1-x0)*fx0/(fx1-fx0)
        fx = f(x)

        print("%4d %10.5f %10.5f %10.5f %10.5f %10.5f %10.5f" %
              (iter, x0, x1, fx0, fx1, x, fx))

        if fx0 * fx < 0:
            x1, fx1 = x, fx
        else:
            x0, fx0 = x, fx

        if iter > 0 and abs(x-x_prev) < threshold:
            # Check for the error after at least one iteration is done
            print("\nHence, the solution is: %10.5lf" % (x))
            return

        iter = iter+1
        x_prev = x

    raise "Max iterations reached"


print("---------Method of False Position---------")
x0 = float(input("Enter x0: "))
x1 = float(input("Enter x1: "))
threshold = float(input("Enter error threshold: "))

false_position(x0, x1, threshold)

Matlab

%% Method of False Position in matlab/octave

MAX_ITER = 100;

% Declare the function
f = @(x) x*x-2;

printf('---------Method of False Position---------\n');

printf('Enter x0: ');
x0 = scanf('%f', 'C');
printf('Enter x1: ');
x1 = scanf('%f', 'C');

fx0 = f(x0);
fx1 = f(x1);

% Check whether the interval brackets a solution
if (fx0 * fx1 >= 0)
  error('The given interval doesn''t bracket a solution\n');
endif

printf('Enter error threshold: ');
threshold = scanf('%f', 'C');

printf('\nSolution:\n');
printf('%4s %10s %10s %10s %10s %10s %10s\n', 'N', 'x0', 'x1', 'f(x0)', 'f(x1)', 'x', 'f(x)');

iter = 0;
x_prev = nan;

% Perform bisection method
while (iter < MAX_ITER)
  x = x0-(x1-x0)*fx0/(fx1-fx0);
  fx = f(x);
  printf('%4d %10.5f %10.5f %10.5f %10.5f %10.5f %10.5f\n', iter + 1, x0, x1, fx0, fx1, x, fx);
  
  % Reassign the interval
  if (fx0 * fx < 0)
    x1 = x;
    fx1 = fx;
  else
    x0 = x;
    fx0 = fx;
  endif

  if (iter > 0 && abs(x-x_prev)<threshold)
    printf('\nHence, the solution is: %10.5f\n', x);
    break;
  endif

  iter++;
  x_prev = x;
endwhile

if (iter>=MAX_ITER)
  error('Max iterations reached');
end

Output

---------Method of False Position---------
Enter x0: 1
Enter x1: 2
Enter error threshold: 0.001

Solution:
   N         x0         x1      f(x0)      f(x1)          x       f(x)
   1    1.00000    2.00000   -1.00000    2.00000    1.33333   -0.22222
   2    1.33333    2.00000   -0.22222    2.00000    1.40000   -0.04000
   3    1.40000    2.00000   -0.04000    2.00000    1.41176   -0.00692
   4    1.41176    2.00000   -0.00692    2.00000    1.41379   -0.00119
   5    1.41379    2.00000   -0.00119    2.00000    1.41414   -0.00020

Hence, the solution is:    1.41414

Convergence

In the regula falsi method, the error decreases by a factor $|c_n|< 1$ after the $n^th$ iteration. The factor $c$ is variable for each iteration but the new error is always proportional to the previous error raised to power 1.

$$e_{n+1}=c_n\cdot e_n$$

Thus, the rate of convergence is variable but the order of convergence is linear. The regula falsi method, on average, converges faster than the bisection method.

Advantages

1. Higher rate of convergence than the bisection method
2. Guaranteed convergence provided the initial conditions are met

Disadvantages

1. More complex than the bisection method.
2. Requires the solution to be bracketed.
3. Order of convergence is linear despite the added complexity.